一串取樣間隔為 0.1 秒的時間訊號為例,如果想以訊號處理方法將訊號間隔增加到 0.025 秒,自然必須以內插加入新資料點。
Linear Interpolation
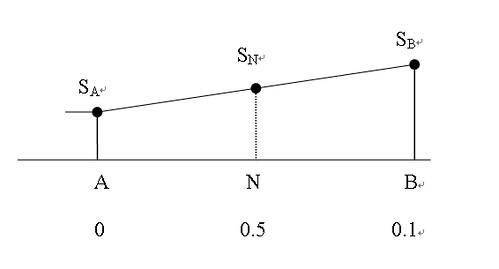
增加資料點最簡單的方式是使用 Linear Interpolation ,其方法是將新取樣點前後想鄰兩原取樣點連線,連線通過新取樣點時間位置時的值即設為新取樣點的值。如下圖所示,A、B為原取樣位置,SA及SB為原取樣位置的取樣值,N為新取樣位置,SN為新取樣位置的取樣值,則SN的計算公式如下︰
Sinc Interpolation
假設一訊號 f(t) 及其頻譜 F(ω) 如下圖︰
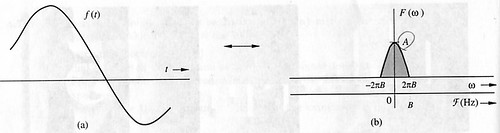
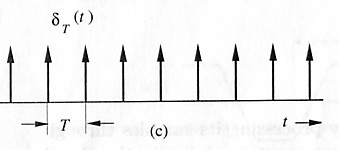
有一個 impulse train δT(t) ,其 pulse 之間的間隔為 T ,其訊號圖如下︰
若訊號 f(t) 以 T 的時間間隔做取樣,則取得取樣後的訊號 f(t) = f(t).δT(t) ,其訊號及頻譜如下︰
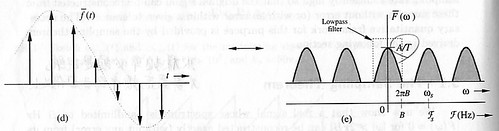
從頻譜的角度來看,訊號的取樣過程會在頻譜上產生週期化的現象。因此若如上圖頻譜圖所示,在取樣後的頻譜上,使用一個頻寬與原訊號頻寬相同的低通濾波器(Lowpass filter)濾波,則又可將取樣後的訊號還原到原訊號。下圖為一理想低通濾波器的頻譜H(ω)及時域圖h(t)︰
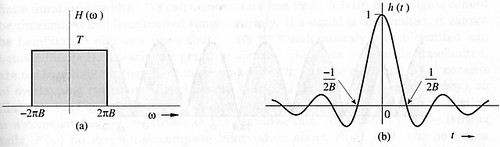
則還原後訊號 fR(t) = f(t) * h(t) ,重建過程及重建後訊號如下圖︰
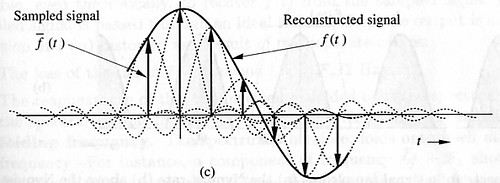
理想的低通濾波器在時域的型式為一 sinc 函數,然而 sinc 是一無限的函數(unbounded function),只能以近似的方式模擬,因此實作時所還原得到的訊號與原訊號仍有差異。
若一取樣間隔為 T1 的離散訊號,欲以 T2 的取樣間隔重新取樣,可假想為將取樣間隔為 T1 的離散訊號以理想低通濾波器還原為原來的連續訊號,再使用 T2 取樣間隔重新取樣,又由於理想的低通濾波器在時域的型式為一 sinc 函數,因此一方法稱為 Sinc Interpolation。
若
f(k1T1)︰原取樣間隔為 T1 的離散訊號
f(k2T2)︰新取樣間隔為 T2 的離散訊號
T1︰原訊號取樣間隔
T2︰新取樣間隔
B︰sinc 函數(or 低通濾波器)的頻寬,T1 = 1/(2B)
則 Sinc Interpolation 的計算公式為︰
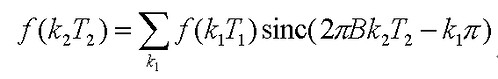
Sinc Interpolation 的 C 程式碼請參考這裡。
參考資料︰
B. P. Lathi, Signal Processing & Linear Systems, Berkeley Cambridge Press, 1998.
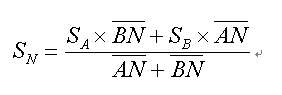



No comments:
Post a Comment